遗传算法的python实现及在量化交易中作用的思考
这篇文章很好地解释了遗传算法,他的代码是用matlab来实现的,为了增加理解,我想把它用python实现了一遍。
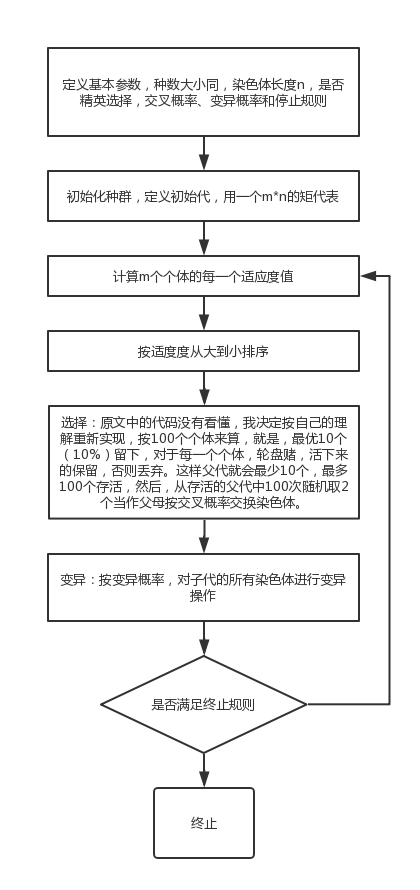
上面的轮盘赌算法,基本思路是,从大到小将适应度排列,然后计算出每个个体占总适应度的比例,再计算出其累积概率,越到后面累积概率值越高,而要求随机数大于它的可能性就越小。
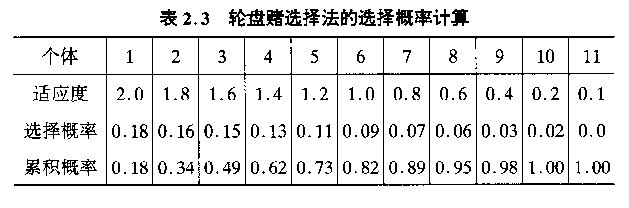
以上图为例,选一个随机数,可以看出,对于个体1来说,有82%的可能性被选中,而对于个体5来说,被选中的概率在27%。
下面是用python写的一个示例代码,从中可以看出适应度如果有小于0的值,计算当前适应度占总适应度比例当作概率时会有问题,这时所有的适应度加一个固定的值,保证适应度全为正,在本例中,为了省事,我将公式修改了一下,在三角函数外加了一个abs(),现在计算用的公式是f(x) = x + abs(10*sin(5*x)) + abs(7*cos(4*x)),来保证值大于0。
import random
import numpy as np
if __name__ == "__main__":
fitness = np.array([[4, 2.0], [3, 1.8], [0, 1.4], [1, 1.2], [2, 1.0], [6, 0.7], [7, 0.3], [5, 0.1]])
sumFits=fitness.sum(axis=0)[1]
i=0
while i<5:
rndPoint = random.uniform(0, sumFits)
accumulator=0
retInd=0
for ind,val in enumerate(fitness):
accumulator += val[1]
if accumulator>=rndPoint:
retInd=val[0]
break
print(sumFits,rndPoint,accumulator,retInd,ind)
i+=1但在我们刚才说的流程中,有另外一个问题,我要的不是对于这些个体,每做一次选择,都得有一个值被选中,而这些值中每个被选中的概率是越向后越小。我们要实现的是,对于每一个个体,我们都做一次是否保留的决策,而保留的概率是,选择概率越大,被保留的概率越大。这使得代码更加简单了:
sumFitness=sum(sortV[int(population_size*elitism_rate):,1])
accumulator = 0 #累积概率
for i in range(int(population_size*elitism_rate),population_size):
rndValue=random.random() #取一个[0,1)之间的随机数
accumulator += sortV[i, 1] /sumFitness
if rndValue>= accumulator:
parent_gen[int(sortV[i,0]), chromosome_size] = 9
else:
parent_gen[int(sortV[i,0]), chromosome_size] = -9最终代码在放在github上。在运行测试时,发现了一个有趣的事实,就是精英比例的问题,如果我把精英比例设的比较大,比如10%,则根本不收敛。
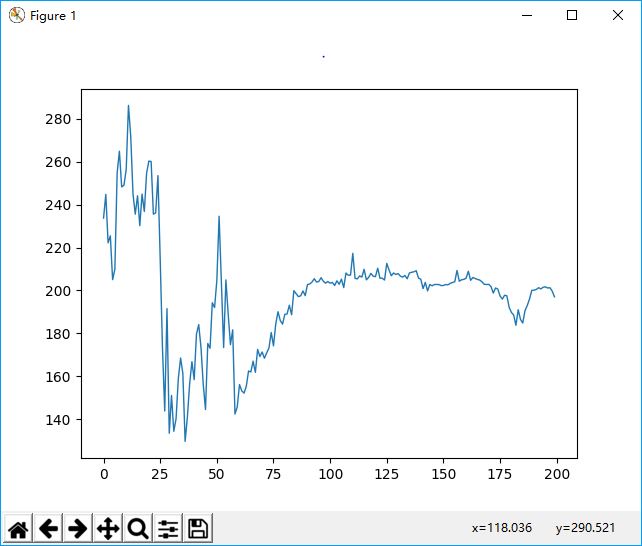
如果精英比例缩小到0.01时,则效果要好看的多,这说明遗传这东西和自然界一样,主要靠变异,关键在于适应性,父母优秀不代替子女优秀。
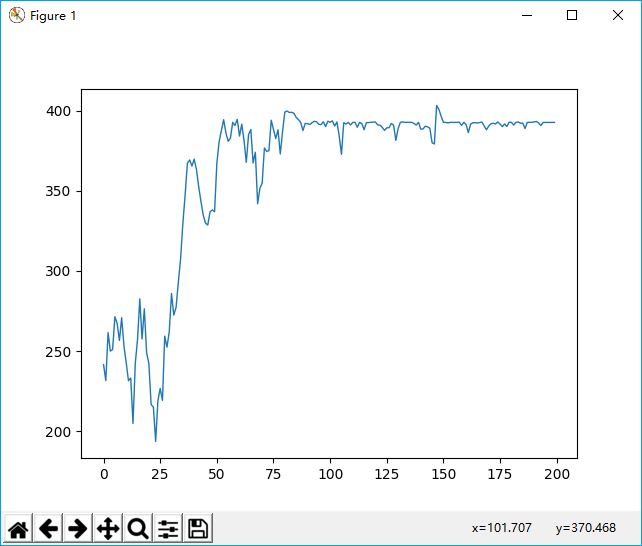
但是整体的收敛效率仍是不高的,可能是代码中还有一些细节搞错了,不过也懒得再查了,只是熟悉了遗传算法的大致原理。
那么在量化交易中如何使用遗传算法呢?
首先,通过进化的方式,找到某种上涨前的规律其实是很低效又不太可行的。那么,用父母来比拟,只能说,一个交易很厉害的父母的子女,继承了他父母的操作习惯,也很厉害。那么这个遗传因子,应该是一个个独立的操作模式,是自洽的封闭的,这样才能遗传才能交换,同时,这些模式又有由多个参数来修饰操作程度,但不至于因为参数变化而发生操作反转,这样才能使变异不至于形成一个操作的振荡状态。
当然,和上例中染色体的操作不同,我们可以想象一个个量化交易的机器节点,每一个节点可能有一个或多种操作模式,这些模式相互独立而又由多个参数来修饰,然后,这些机器节点通过一段时间的操作,根据收益率来进行淘汰,存活下来的节点,再与其它的节点相互溶合,随机地增加或减少操作模式点,从而产生下一代的节点。
而在具体实现上,从《自然计算:DNA、量子比特和智能机器的未来》一书中,可以看一个简单的概念性例子:
例如,假设收益规则1表述为:
如果1分钟的交易价格变化率>5%,且5分钟的交易规模变化率>10%,则买入。
而获利规则2表述为:
如果2分钟的交易价格变化率>5%,且10分钟的交易规模变化率<20%,则买入。
那么从这两条规则中能生成什么样的新规则呢?又如何对它们进行组合?你可能会随机地交换这两条规则的要素,来生成规则3:
如果2分钟的交易价格变化率>5%,且5分钟的交易规模变化率>10%,则买入。
或者也可以通过改变属性值来修改获利规则,如,将规则2中“2分钟的变化率”属性从5%改为10%,从而产生规则4:
如果2分钟的交易价格变化率>10%,且10分钟的交易规模变化率<20%,则买入。
洛夫莱斯使用了一些经典的规则搜索策略:如精英选择(classical elite selection)、局部平移(local shifting)、禁忌约束交叉(tabuconstrained crossover)等,以及在此基础上他自己发明的若干策略,并将这些策略与不同的适应度标准进行组合。针对每种组合方式都尝试构建一个解决方案的集合。当每一代的运算或每一次的迭代结束时,所有组合方式所产生的所有解决方案,都经过了评估及重组。
有些重组方法只是简单地根据得分的高低来交换属性及属性值,但洛夫莱斯显然想得到一个更加通用的系统。他解释说:“最终我们建立了一个通用的进化计算框架,可以并行处理大量的重组方法及不同的优化函数。”在每一代的计算结束时,所有搜索方法共享进化的结果,然后由一个第二级的启发式算法为下一代的搜索方法分配资源。
